Areas of a spatial segregation model significantly different from null expectations
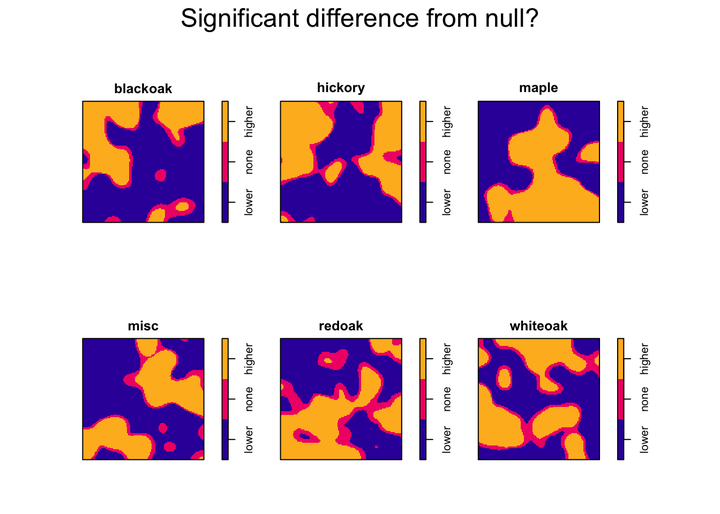 Image credit: Ian Buller
Image credit: Ian Buller
I present code to identify areas of a spatial segregation model that exceed our null expectations using the relrisk function in the spatstat package and an assumption of normality of the estimated probabilities. A spatial segregation model was originally proposed by Diggle, Zheng, & Durr in 2005 which estimates spatially-varying probabilities of an event of a certain type to occur in an area accounting for other types. The original method uses a Monte Carlo-based simulation, which is computationally expensive. Instead, Adrian Baddeley and the spatstat team adapted the relrisk function for a multitype (m > 2) point pattern that has an option to compute the standard error of the probability estimates based on asymptotic theory, assuming a Poisson process.
Here, I use the standard errors to compute a 95% confidence interval (CI) at all gridded pixels (“knots”) for each type. Knots with a CI that does not capture the null expectation for each type are identified. I use the provided lansing dataset from the spatstat.data package. Created with assistance from Dr. Lance Waller and Barry Rowlingson.
# Packages
loadedPackages <- c("spatstat.core", "spatstat.geom", "spatstat.data", "spatstat")
invisible(lapply(loadedPackages, require, character.only = T))# Data
spatstat.data::lansing## Marked planar point pattern: 2251 points
## Multitype, with levels = blackoak, hickory, maple, misc, redoak, whiteoak
## window: rectangle = [0, 1] x [0, 1] units (one unit = 924 feet)# Convert the lansing data to a ppp object
ppp_lansing <- spatstat.geom::ppp(x = spatstat.data::lansing$x,
y = spatstat.data::lansing$y,
window = spatstat.geom::unit.square(),
marks = as.factor(spatstat.geom::marks(spatstat.data::lansing)))
# Plot input
spatstat.geom::plot.ppp(ppp_lansing, main = "Lansing Woods", cex = 0.5)
# Estimate nonparametric spatially-varying probabilities of type
f1 <- spatstat.core::relrisk.ppp(ppp_lansing, casecontrol = F, diggle = T, se = T, sigma = bw.diggle)
# Default plots
plot(f1$estimate, main = "Probability of an event by type", zlim = c(0,1)) # probabilities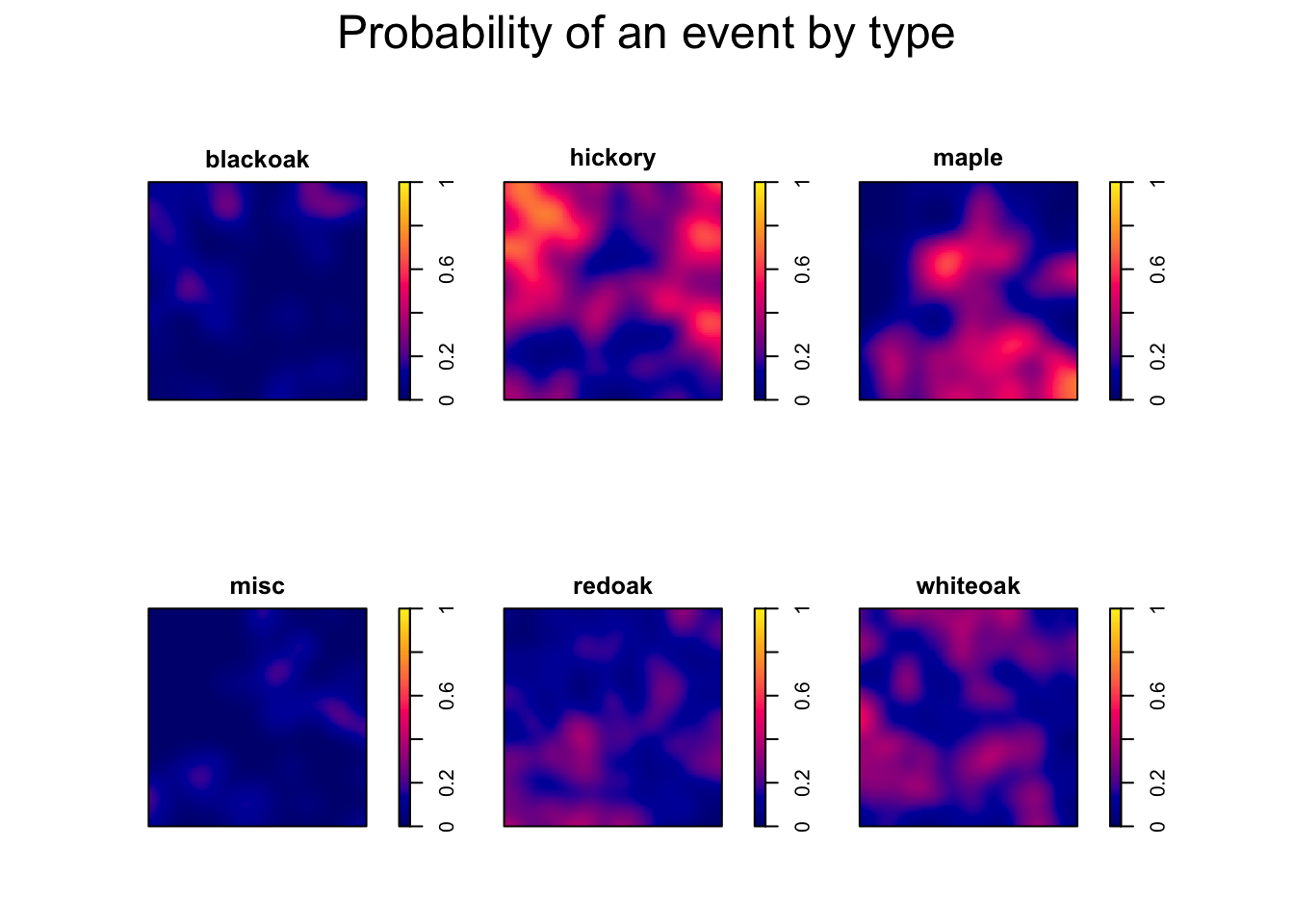
plot(f1$SE, main = "Standard error of probability", zlim = c(0,0.03)) # standard errors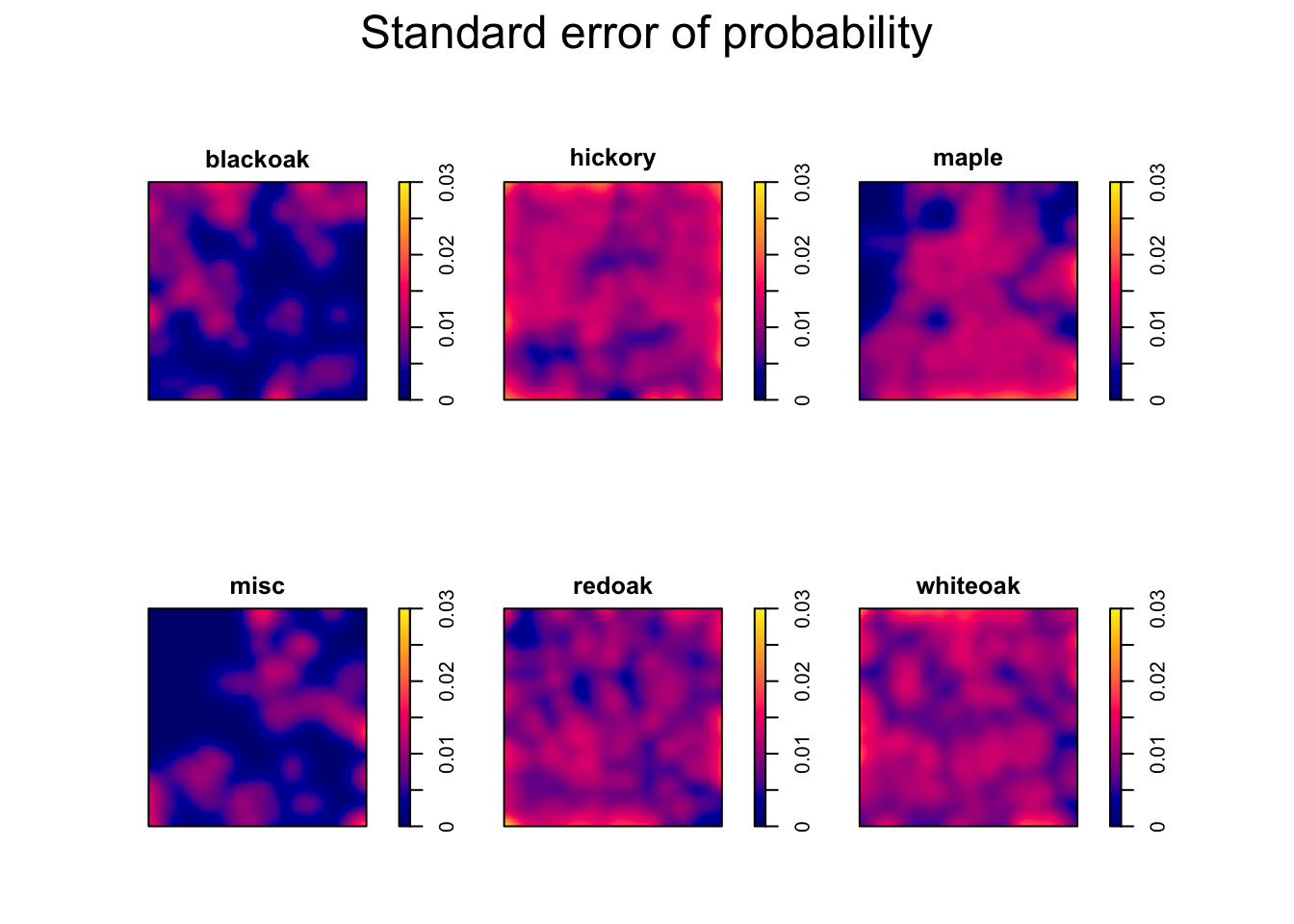
wh <- spatstat.geom::im.apply(f1$estimate, which.max)
types <- levels(spatstat.geom::marks(spatstat.data::lansing))
wh <- spatstat.geom::eval.im(types[wh]) # most common
spatstat.geom::plot.im(wh, main="Most common species", ribargs = list(las = 1))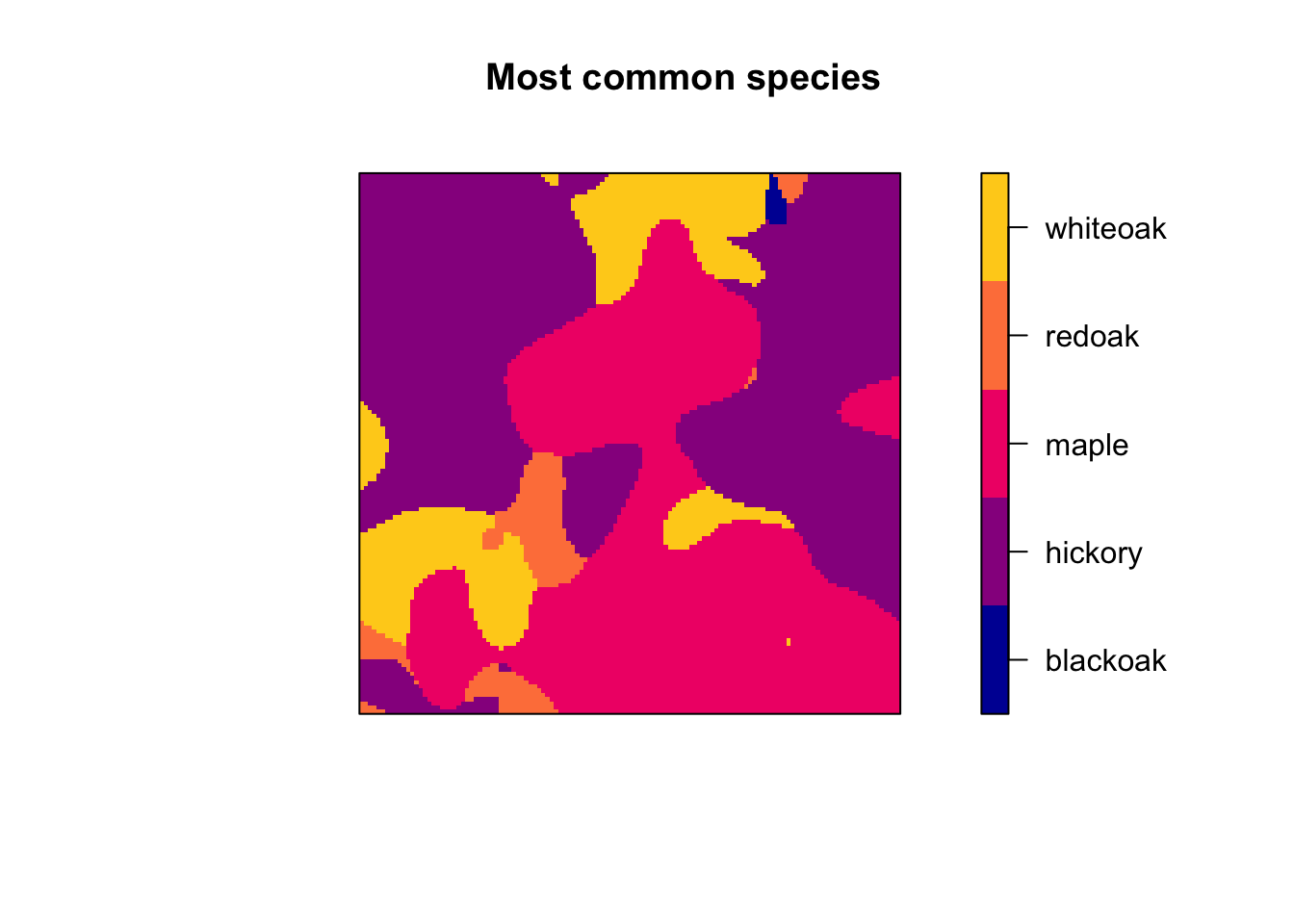
# Significant p-values assumming normality of the Poisson process
## relrisk() computes standard errors based on asymptotic theory, assuming a Poisson process
alpha <- 0.05 # alpha
z <- qnorm(alpha/2, lower.tail = F) # z-statistic
f1$u <- f1$estimate + z*f1$SE # Upper CIs
f1$l <- f1$estimate - z*f1$SE # Lower CIs
mu_0 <- as.vector(table(spatstat.geom::marks(ppp_lansing))/ppp_lansing$n) # null expectations by type
f1$p <- f1$estimate # copy structure of pixels, replace values
for (i in 1:length(f1$p)) {
f1$p[[i]]$v <- factor(ifelse(mu_0[i] > f1$u[[i]]$v, "lower",
ifelse( mu_0[i] < f1$l[[i]]$v, "higher", "none")),
levels = c("lower", "none", "higher"))
}
# Plot significant p-values
plot(f1$p, main = "Significant difference from null?")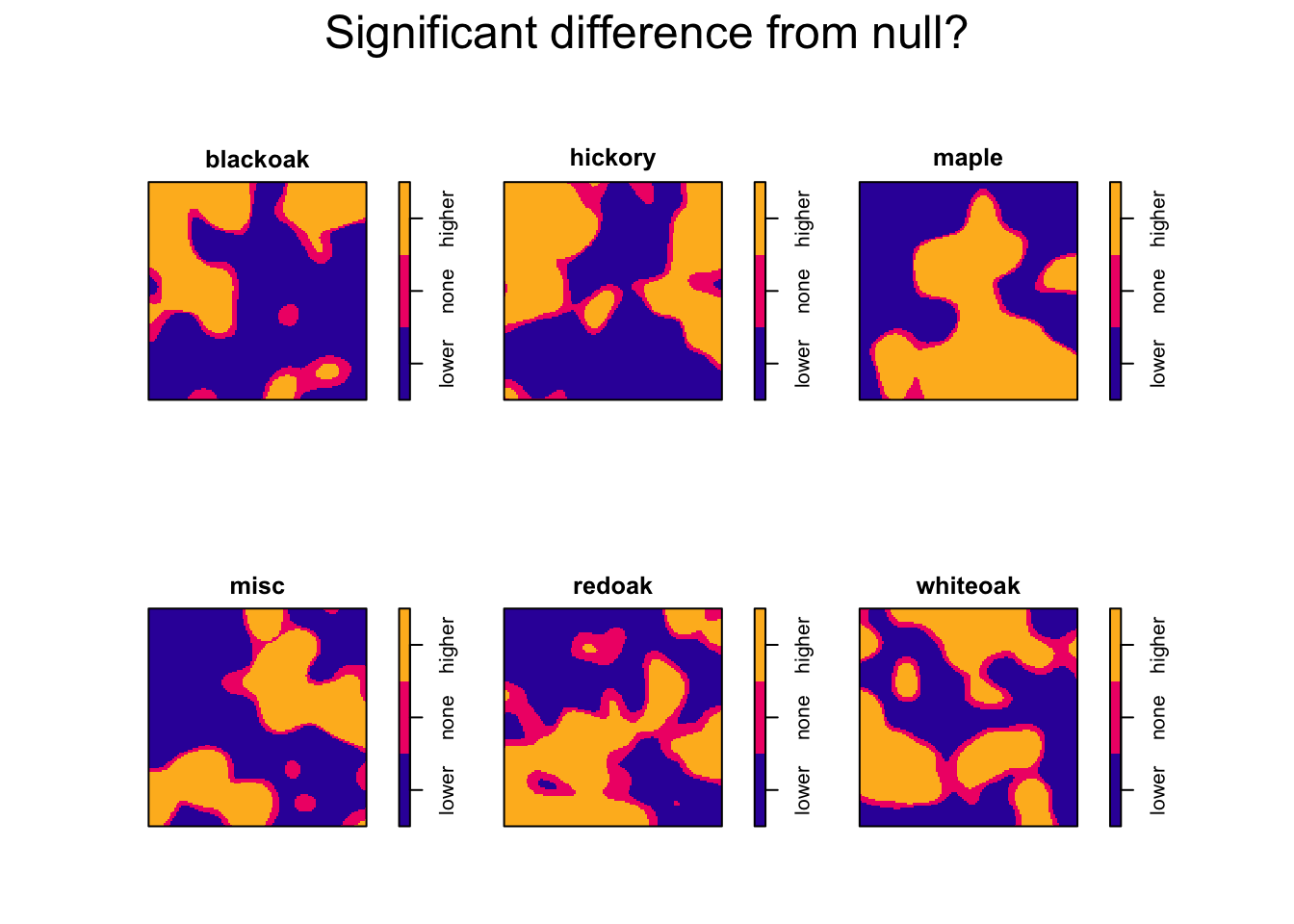
The final plot identifies where the spatially-varying probabilities exceed the null expected probability of each type. Areas of higher-than-expected probability could be considered “hot-spots” and areas of lower-than-expected probability could be considered “cold-spots.” Areas that are not significantly different from the null expectation could suggest additional sampling is necessary to determine if these areas are hot or cold spots.